二叉搜尋樹概念

二叉搜尋樹又稱二叉排序樹，它可能是一棵空樹，或者是具有以下性質的二叉樹

1. 左子樹如果不為空，則左子樹的值一定小於等於根節點
2. 右子樹如果不為空，則右子樹的值一定大於等於根節點
3. 每個根節點的左右子樹也滿足以上性質

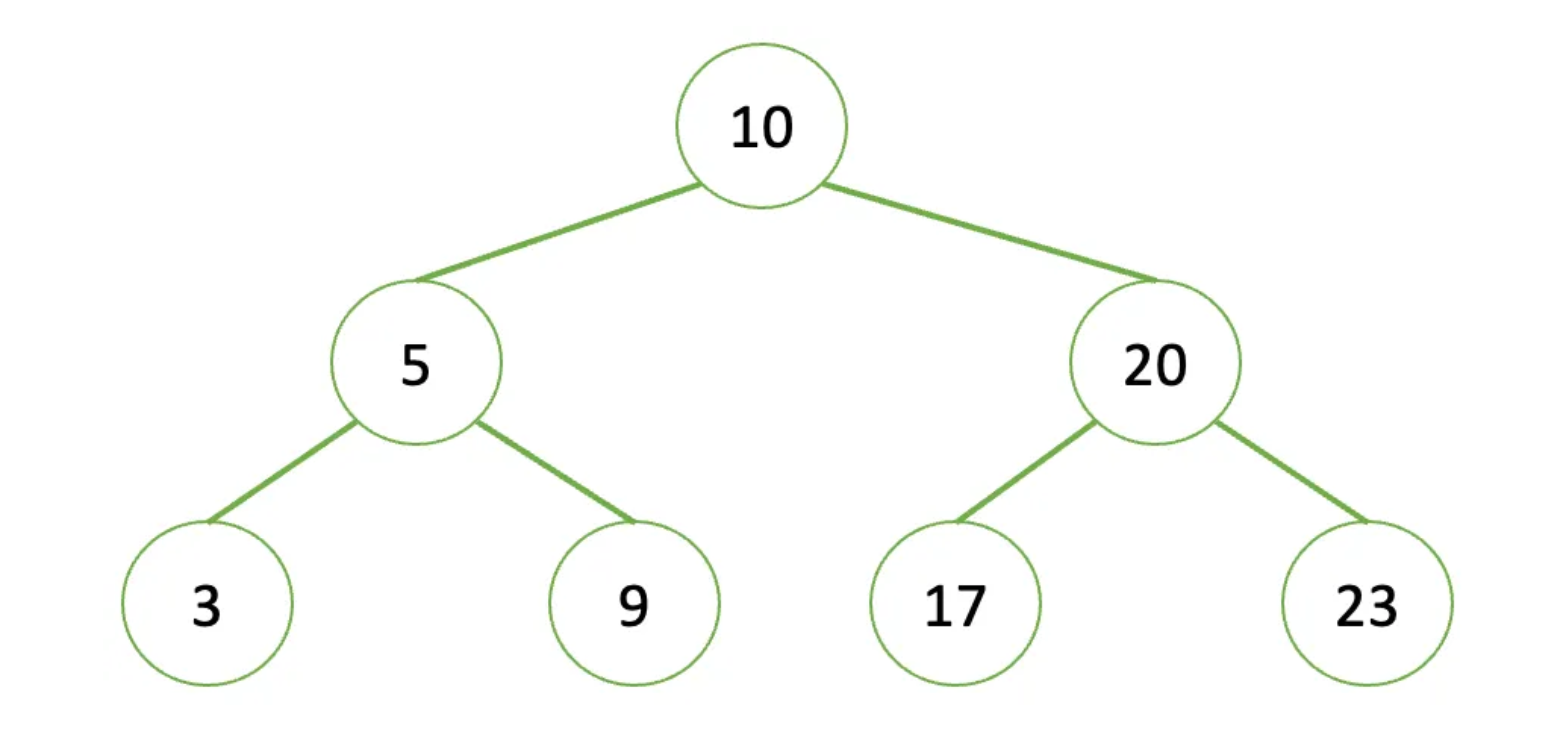
二叉搜尋樹時間複雜度分析

1. 最優情況：二叉搜尋樹整個樹的結構為完全二叉樹或接近完全二叉樹 => O(logN) ( 其中 N 為樹的高度 )

2. 最壞情況：如果插入的資料的順序接近或就是有序也就是說樹的結構接近單枝 => O (N)

   如下圖所示

   

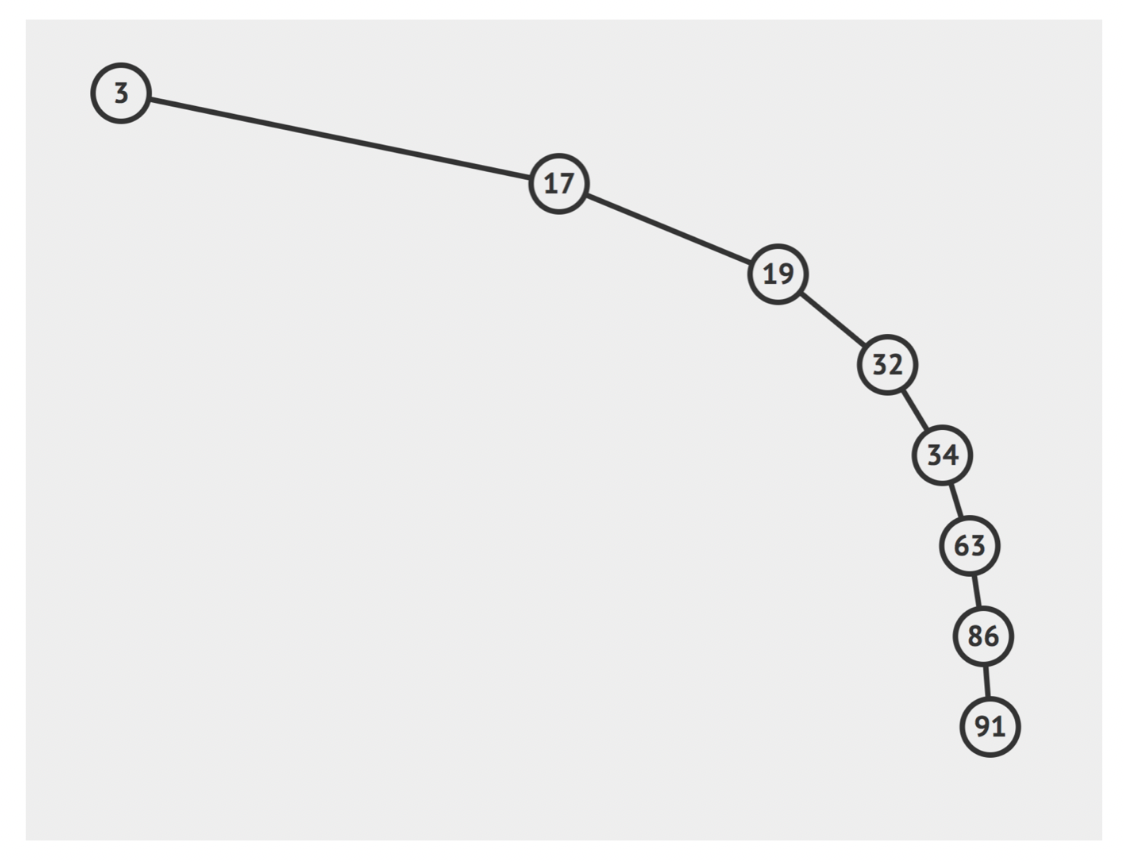
   3. 平均情況：O(N)
   4. 給定一棵二叉搜尋樹，根據節點值大小排序所需時間複雜度是線性的 => 中序遍歷一次就是有序的 (O(N))

二分搜尋 vs. 二叉搜尋樹

二分搜尋的效率也可以達到 O(logN) 但二分搜尋的缺陷有：

1. 需要儲存在支援下標隨機存取的結構中，並且有序
2. 插入和刪除資料效率很低，因為儲存在下標隨機存取的結構中，插入和刪除資料一般需要挪動資料。

因此可以進一步拓展至平衡二叉搜尋樹。在本篇博客不會討論到平衡二叉搜尋樹，只會討論普通的二叉搜尋樹

二叉搜尋樹模擬實現

基本結構

1. 節點 ( BSTNode )

template <class K>
  struct BSTNode{

    BSTNode(const K& value):_left(nullptr),_right(nullptr),_val(value){}
    // 一個節點有哪些數據？
    BSTNode<K>* _left; // 左子
    BSTNode<K>* _right; // 右子
    K _val; // 這個節點的數據
  };
/*
之所以定義為struct 是因為如果定義成類別，預設是私有，如果我們BST的類別要訪問BSTNode的成員就必須把BSTNode設為BST的友元
這樣有點麻煩。而且如果直接把BSTNode struct 其實也只是曝露個BST而已。
*/

2. BST

template <class K>
  class BST{
    public:
    typedef BSTNode<K>* Node;

    private:
    Node* _root = nullptr; //根節點
  };

3. 遍歷 ( 中序遍歷 )

private:
void _InOrder(Node* _root){
  if(_root == nullptr){
    return;
  }
  _InOrder(_root->_left);
  cout << _root-> _val << " " <<  endl;
  _InOrder(_root->_right);
}
public:
void InOrder()
{
  _InOrder(_root);
  cout << endl;
}

插入

插入我們要分兩種情況

1. 根節點為空
2. 根節點不為空

// 插入節點（不允許重複）
bool insert(const K &value)
{
  if (_root == nullptr)
  {
    _root = new BSTNode<K>(value);
    return true;
  }

  Node parent = nullptr;
  Node cur = _root;
  while (cur)
  {
    if (cur->_val < value)
    {
      parent = cur;
      cur = cur->_right;
    }
    else if (cur->_val > value)
    {
      parent = cur;
      cur = cur->_left;
    }
    else
    {
      return false; // 已存在
    }
  }

  // cur 是 nullptr，此時 parent 是插入點的父節點
  Node newNode = new BSTNode<K>(value);
  if (value < parent->_val)
  {
    parent->_left = newNode;
  }
  else
  {
    parent->_right = newNode;
  }

  return true;
}

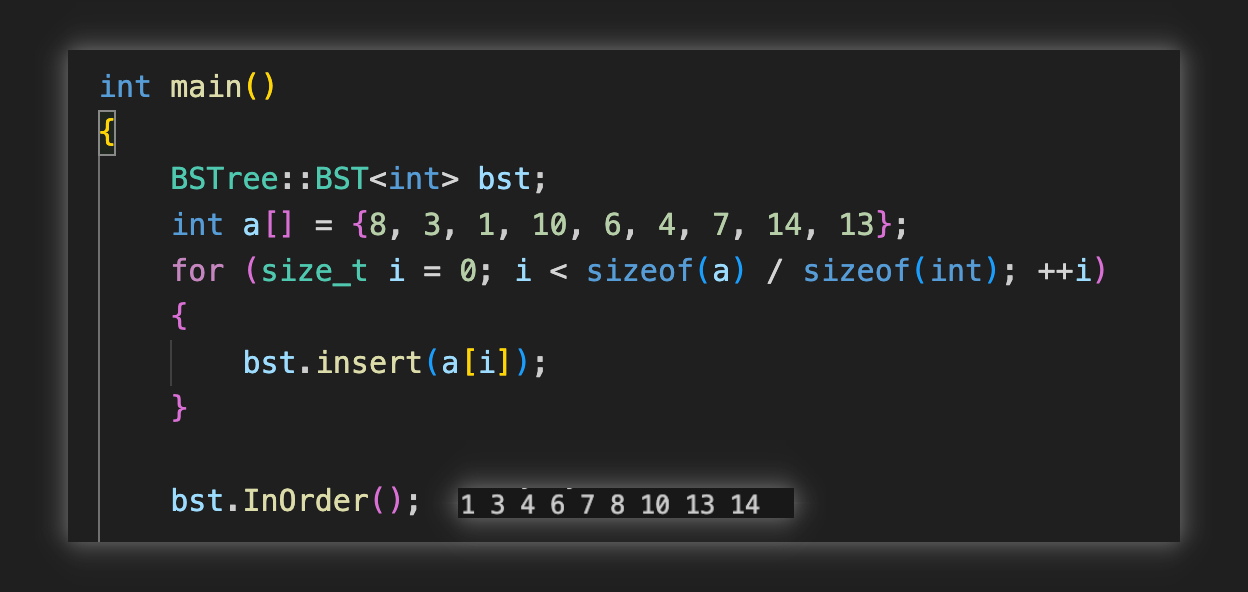
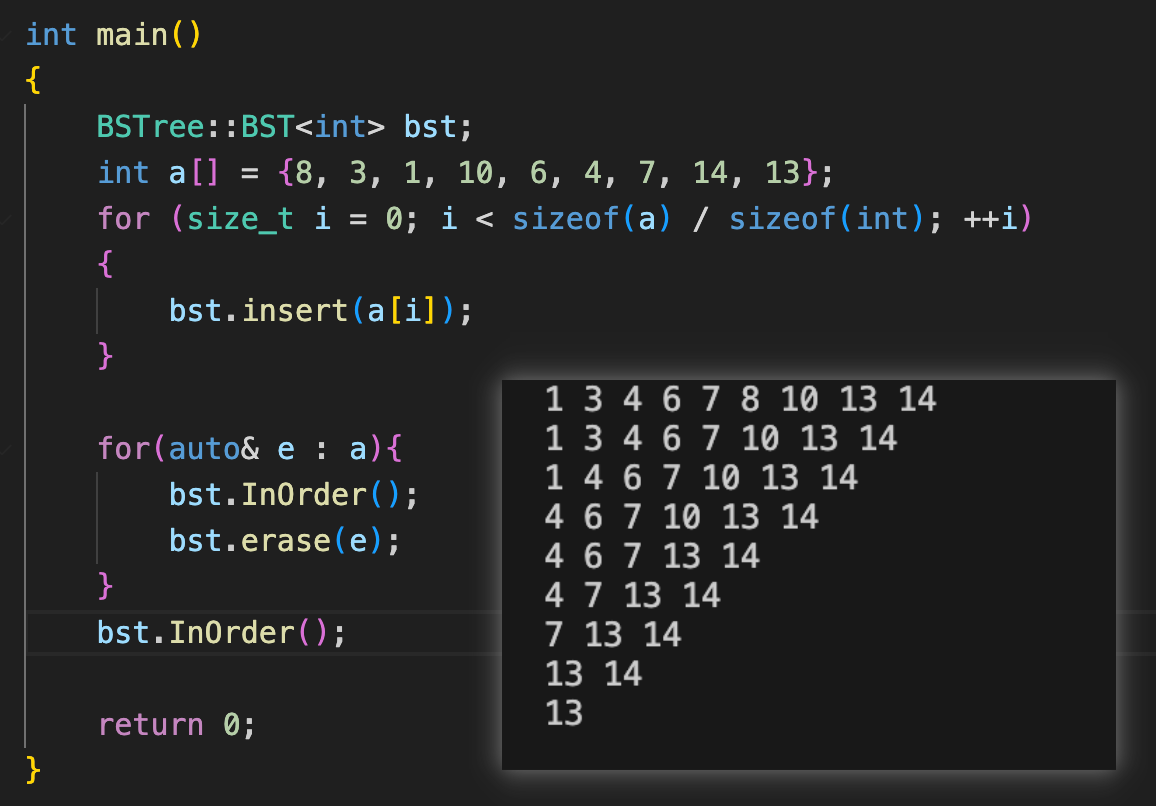
測試用例與結果：

查找

// 查找的邏輯比較簡單，和插入的邏輯大同小異
bool find(const K& value){
      Node* cur = _root;
      while(cur){
      if(cur->_val < value){
        cur = cur->_right;
      }
      else if(cur->_val > value){
        cur = cur->_left;
      }
      else{ // 到這裡代表 cur->_val == value 就直接return true;
        cout << value << " 存在" << endl;
        return true;
      }
      cout << value << " 不存在" << endl;
        return false;
  
}

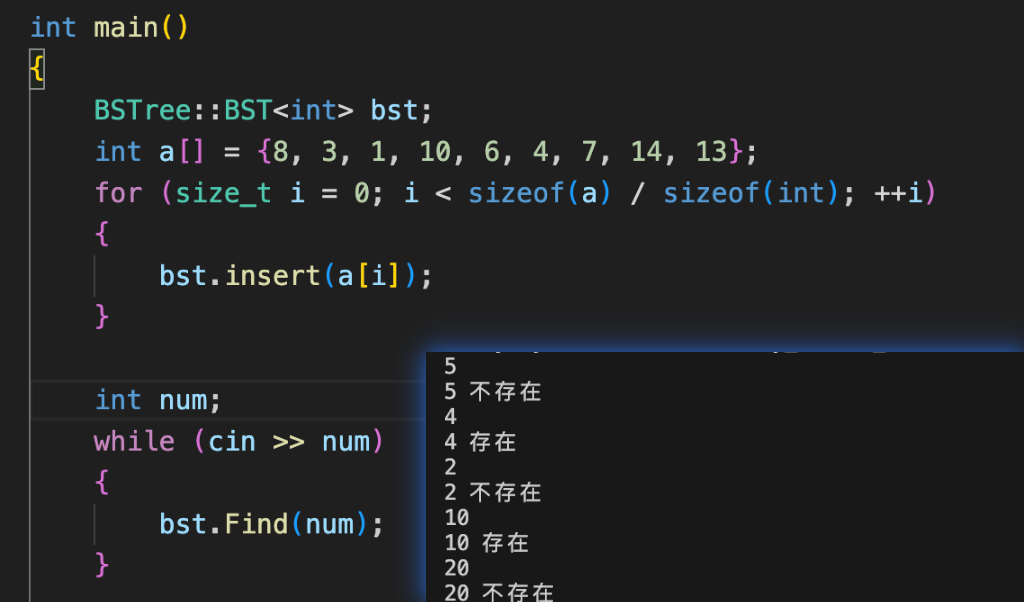
測試用例與結果

刪除

刪除會比較複雜，我們先分析刪除有哪些情況

如果查找元素存在則分以下四種情況分別處理：（假設要刪除的結點為N）

1. 要刪除節點N的左右孩子均為空
2. 要刪除的節點N左孩子位空，右孩子結點不為空
3. 要刪除的節點N右孩子位空，左孩子結點不為空
4. 要刪除的節點N左右孩子結點均不為空

然後再進一步發現 1 2 3 三種情況可以一起處理。所以我們要處理的就只有 (123) 和 (4) 兩種情況

那在刪除的過程中還要確保依然滿足二叉搜尋樹的性質

我們的處理方案：

• 需要獨立處理的情況：如果要刪除的是根節點 => 沒有父節點

• 如果 N 的左孩子為空

  • 如果 N 是 父節點的左孩子 => 父節點的左孩子指向 N 的右孩子
  • 如果 N 是 父節點的右孩子 => 父節點的右孩子指向 N 的右孩子

• 如果 N 的右孩子為空

  • 如果 N 是 父節點的左孩子 => 父節點的左孩子指向 N 的左孩子
  • 如果 N 是 父節點的右孩子 => 父節點的左孩子指向 N 的左孩子

• 如果左右孩子均不為空

  • 選擇 N 節點的左子樹中最大的值 或 選擇 N 節點的右子樹中的最小的值
  • 在將其與節點 N 交換在刪除

bool Erase(const K& val){
  if (_root == nullptr) {
    return false;
  }

  Node* parent = nullptr;
  Node* cur = _root;

  while (cur) {
    if (cur->_val < val) {
      parent = cur;
      cur = cur->_right;
    } else if (cur->_val > val) {
      parent = cur;
      cur = cur->_left;
    } else { // cur->_val == val
      // case 1: 沒有左子樹
      if (cur->_left == nullptr) {
        if (parent == nullptr) {
          _root = cur->_right;
        } else {
          if (parent->_left == cur) {
            parent->_left = cur->_right;
          } else {
            parent->_right = cur->_right;
          }
        }
        delete cur;
        return true;
      }
      // case 2: 沒有右子樹
      else if (cur->_right == nullptr) {
        if (parent == nullptr) {
          _root = cur->_left;
        } else {
          if (parent->_left == cur) {
            parent->_left = cur->_left;
          } else {
            parent->_right = cur->_left; 
          }
        }
        delete cur;
        return true;
      }
      // case 3: 有左右子樹，選右子樹最小節點替代
      else {
        Node* RightMinP = cur;
        Node* RightMin = cur->_right;
        while (RightMin->_left) {
          RightMinP = RightMin;
          RightMin = RightMin->_left;
        }
        cur->_val = RightMin->_val; // 替代值

        // 調整 RightMinP 的連結
        if (RightMinP->_left == RightMin) {
          RightMinP->_left = RightMin->_right;
        } else {
          RightMinP->_right = RightMin->_right;
        }

        delete RightMin;
        return true;
      }
    }
  }

  return false; // val 不存在
}

測試用例與結果

其他

// 0. 預設構造
BST() = default;

// 1. 拷貝構造 => 深拷貝
BST(const BST<K> &bst)
{
  _root = Copy(bst._root);
}
Node *Copy(Node *root)
{
  if (root == nullptr)
  {
    return nullptr;
  }
  Node *Newroot = new Node(root->_key);

  Newroot->_left = Copy(root->_left);
  Newroot->_right = Copy(root->_right);

  return Newroot;
}

// 2. 賦值
BST<K> &operator=(BST<K> target)
{
  std::swap(_root, target._root);
  return *this;
}

// 3. 析構
~BST()
{
  Destroy(_root);
  _root = nullptr;
}
void Destroy(Node *root)
{
  if (root == nullptr)
  {
    return;
  }
  Destroy(root->_left);
  Destroy(root->_right);
  delete root;
}

知識拓展

二叉搜尋樹可以應用在：字典、統計等方面。以下程式碼屬於上面的拓展 ( 只提供有修改的部分 )

template <class K,class V>
  struct BSTNode{

    BSTNode(const K& key,const V& val):_left(nullptr),_right(nullptr),_key(key),_val(val){}
    BSTNode<K,V>* _left; // 左子
    BSTNode<K,V>* _right; // 右子
    K _key; 
    V _val;
  };
template <class K,class V>
  class BST{
    public:
    typedef BSTNode<K,V>* Node;

    private:
    Node _root = nullptr; //根節點
  };
/* ---------------------------------------------------------------------------------------------------- */
bool insert(const K &key, const V &val)
{
  if (_root == nullptr)
  {
    _root = new Node(key, val);
    return true;
  }

  Node *parent = nullptr;
  Node *cur = _root;
  while (cur)
  {
    if (key < cur->_key)
    {
      parent = cur;
      cur = cur->_left;
    }
    else if (key > cur->_key)
    {
      parent = cur;
      cur = cur->_right;
    }
    else
    {
      return false; // 重複 key
    }
  }

  Node *newNode = new Node(key, val);
  if (key < parent->_key)
    parent->_left = newNode;
  else
    parent->_right = newNode;

  return true;
}
/* ---------------------------------------------------------------------------------------------------- */
void _InOrder(Node *root)
{
  if (root == nullptr)
  {
    return;
  }
  _InOrder(root->_left);
  cout << root->_key << ":" << root->_val << endl;
  _InOrder(root->_right);
}
/* ---------------------------------------------------------------------------------------------------- */
Node *find(const K &key)
{
  Node *cur = _root;
  while (cur)
  {
    if (key < cur->_key)
      cur = cur->_left;
    else if (key > cur->_key)
      cur = cur->_right;
    else
    {
      return cur;
    }
  }
  return nullptr;
}

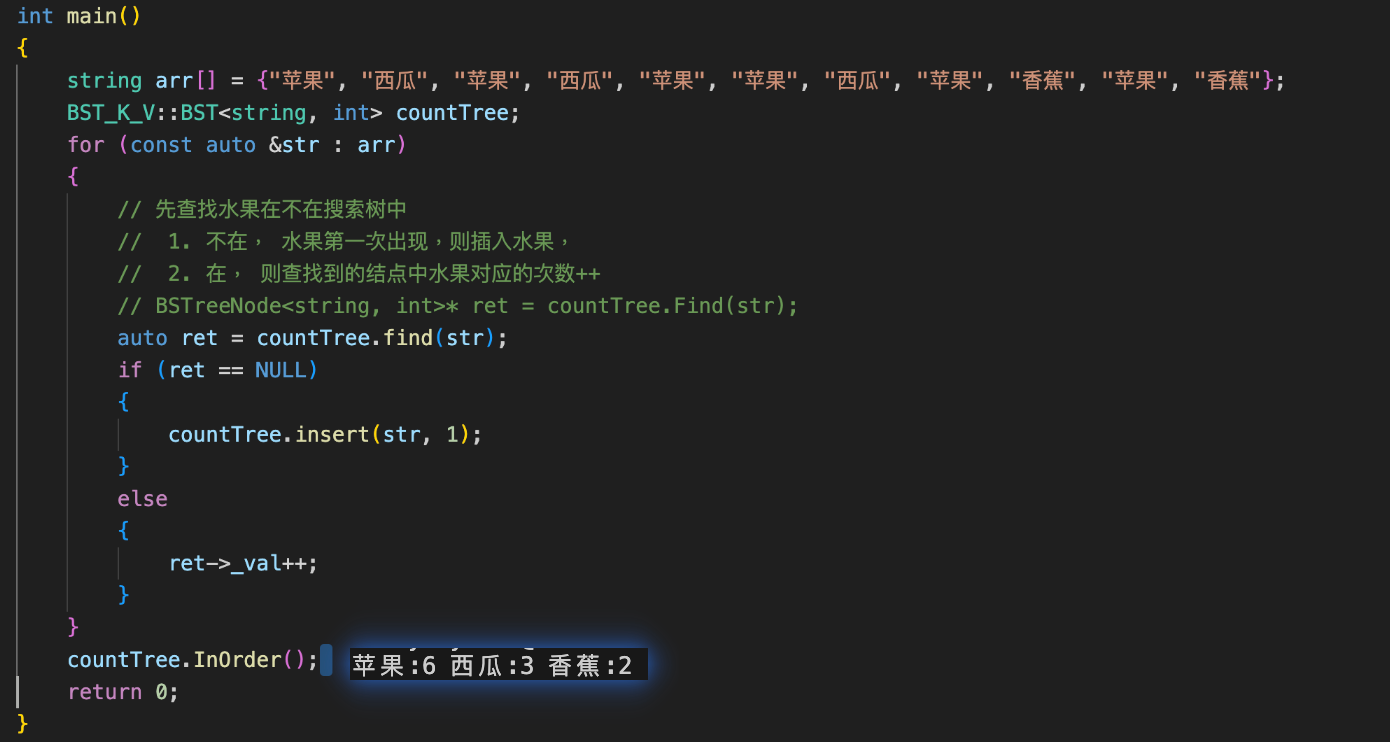
測試案例與結果

BST與AVL轉換

BST轉換為AVL樹

將普通BST轉換為AVL樹的核心思想：

1. 中序遍歷BST獲得有序序列
2. 清空當前BST樹
3. 將有序序列重新插入AVL樹中

// AVL節點結構（用於轉換）
template <class K, class V>
struct AVLNode {
AVLNode(const pair<K, V>& kv) 
 : _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0) {}
AVLNode<K, V>* _left;
AVLNode<K, V>* _right;
AVLNode<K, V>* _parent;
pair<K, V> _kv;
int _bf; // 平衡因子
};

// BST轉換為AVL樹的函數
AVLNode<K, V>* ConvertToAVL() {
// 步驟1：中序遍歷BST，收集所有節點值
vector<K> values;
_InOrderCollect(_root, values);

// 步驟2：創建新的AVL樹
AVLNode<K, V>* avlRoot = nullptr;

// 步驟3：將收集到的值插入AVL樹
for (const K& value : values) {
 avlRoot = _InsertAVL(avlRoot, make_pair(value, V{}));
}

return avlRoot;
}

private:
// 中序遍歷收集節點值
void _InOrderCollect(Node* root, vector<K>& values) {
if (root == nullptr) {
 return;
}
_InOrderCollect(root->_left, values);
values.push_back(root->_val);
_InOrderCollect(root->_right, values);
}

// 向AVL樹插入節點（簡化版本，不包含旋轉）
AVLNode<K, V>* _InsertAVL(AVLNode<K, V>* root, const pair<K, V>& kv) {
if (root == nullptr) {
 return new AVLNode<K, V>(kv);
}

if (kv.first < root->_kv.first) {
 root->_left = _InsertAVL(root->_left, kv);
 root->_left->_parent = root;
} else if (kv.first > root->_kv.first) {
 root->_right = _InsertAVL(root->_right, kv);
 root->_right->_parent = root;
}

return root;
}

AVL轉換為BST

將AVL樹轉換為普通BST的核心思想：

1. 中序遍歷AVL樹獲得有序序列
2. 創建新的BST樹
3. 將有序序列插入BST中

// 將AVL樹轉換為BST
void ConvertFromAVL(AVLNode<K, V>* avlRoot) {
// 步驟1：清空當前BST樹
_Destroy(_root);
_root = nullptr;

// 步驟2：中序遍歷AVL樹，收集所有節點值
vector<K> values;
_InOrderCollectAVL(avlRoot, values);

// 步驟3：將收集到的值重新插入BST
for (const K& value : values) {
 insert(value);
}
}

private:
// 中序遍歷AVL樹收集節點值
void _InOrderCollectAVL(AVLNode<K, V>* root, vector<K>& values) {
if (root == nullptr) {
 return;
}
_InOrderCollectAVL(root->_left, values);
values.push_back(root->_kv.first); // 收集鍵值
_InOrderCollectAVL(root->_right, values);
}

// 銷毀BST樹
void _Destroy(Node* root) {
if (root == nullptr) {
 return;
}
_Destroy(root->_left);
_Destroy(root->_right);
delete root;
}

轉換測試示例

// 測試轉換功能
void TestBSTConversion() {
// 創建一個不平衡的BST
BST<int> bst;
bst.insert(5);
bst.insert(3);
bst.insert(7);
bst.insert(1);
bst.insert(4);
bst.insert(9);
bst.insert(10);

cout << "原始BST中序遍歷: ";
bst.InOrder();

// 轉換為AVL樹
AVLNode<int, int>* avlRoot = bst.ConvertToAVL();
cout << "轉換後的AVL樹中序遍歷: ";
_PrintAVLInOrder(avlRoot);
cout << endl;

// 轉換回BST
BST<int> newBST;
newBST.ConvertFromAVL(avlRoot);
cout << "轉換回BST的中序遍歷: ";
newBST.InOrder();
}

private:
// 打印AVL樹中序遍歷
void _PrintAVLInOrder(AVLNode<K, V>* root) {
if (root == nullptr) {
 return;
}
_PrintAVLInOrder(root->_left);
cout << root->_kv.first << " ";
_PrintAVLInOrder(root->_right);
}

轉換複雜度分析

時間複雜度：

• BST轉AVL：O(N log N)

  • 中序遍歷：O(N)
  • 重新插入：O(N log N)（每次插入O(log N)，共N次）

• AVL轉BST：O(N log N)

  • 中序遍歷：O(N)
  • 重新插入：O(N log N)

空間複雜度：O(N)

• 需要額外空間存儲中序遍歷結果
• 遞歸調用棧空間：O(log N)

轉換的優缺點：

• 優點： 保證轉換後的樹結構正確，數據順序保持一致
• 缺點： 時間複雜度較高，需要重新構建整棵樹
• 注意： BST轉AVL後會失去平衡性，需要額外的平衡調整